小型精刨机主切削运动机构

项目背景

牛头刨床是一个靠刀具的往复直线运动及工作台的间歇运动来完成工件的平面切削加工的机床。

设计要求

要求主切削运动机构能使刨刀作往复直线运动。在工作行程时，刨刀速度要平稳，近可能接近等速，在空回行程时，刨刀快速退回，即要有急回作用。具有良好的传力性能，结构简单，动作轻便灵活。主要设计参数如下：

  • 直线刨削行程: H=400mm
  • 工件刨削长度: L=320MM
  • 行程速比系数: K=1.41
  • 每分钟往复切削运动的次数 n=72次/min
  • 切削阻力: Fr=4500N
  • 滑枕导路支承面离安装平面的距离需控制在1000mm之内。

使用解析法完成设计

首先我们先对于下面的摇杆进行抽象出一个数学模型：

位置分析

具体的数学物理分析其位置如下：

速度分析

通过上面的模型再进行速度分析：

加速度分析

对于刨刀架进行分析

对于导杆结构进行分析

主动杆的分析

总结

通过解析法的分析，我们可以得出以下几点结论：

使用 SW 进行仿真分析

通过这个模型进行 3D 建模，同时使用 SW 进行仿真分析，可以得到以下的结果：

运行效果如下：

Matlab 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
clc;clear;close all;

%% 基本数据条件
l1 = 92.4;
l6 = 350;
l3 = 757.4;
omegal1 = -2.4*pi;
H1 = 100;
G3 = 200;
G5 = 700;
J_s3 = 1.1;
l_s3 = l3/2;
g = 10;


disp("代码说明:x右为0度,涉及转动的,逆时针为正,笛卡尔坐标系")


ifzu = input('你是组长吗?,是为1,不是为0\n');
if ifzu == 1
MyPar = parpool; 
ifzhouqi = input('周期绘图?,是为1,不是为0\n');

        if ifzhouqi == 1
            nzhouqi = input('几个周期?\n');
            v = [];
            a = [];
            s = [];
            Mb = [];
            for i = -nzhouqi*2:0.01:0
                phy1 = pi*i;
                [vi,ai,si,Mb_i] = sol_wzr(l1,l6,l3,omegal1,phy1,G5,G3,g,l_s3,J_s3);
                v = [v,vi];
                a = [a,ai];
                s = [s,si];
                Mb = [Mb,Mb_i];
            end  
            phy1_n = (-nzhouqi*2:0.01:0)*pi;
        end
        if ifzhouqi == 0
            v = [];
            a = [];
            s = [];
            Mb = [];
            for i = -2:0.001:0
                phy1 = pi*i;
                [vi,ai,si,Mb_i] = sol_wzr(l1,l6,l3,omegal1,phy1,G5,G3,g,l_s3,J_s3);
                v = [v,vi];
                a = [a,ai];
                s = [s,si];
                Mb = [Mb,Mb_i];
            end  
            phy1_n = (-2:0.001:0)*pi;
        end

%% 绘图
    % 设置背景颜色
    set(gcf, 'Color', [1 1 1]);  
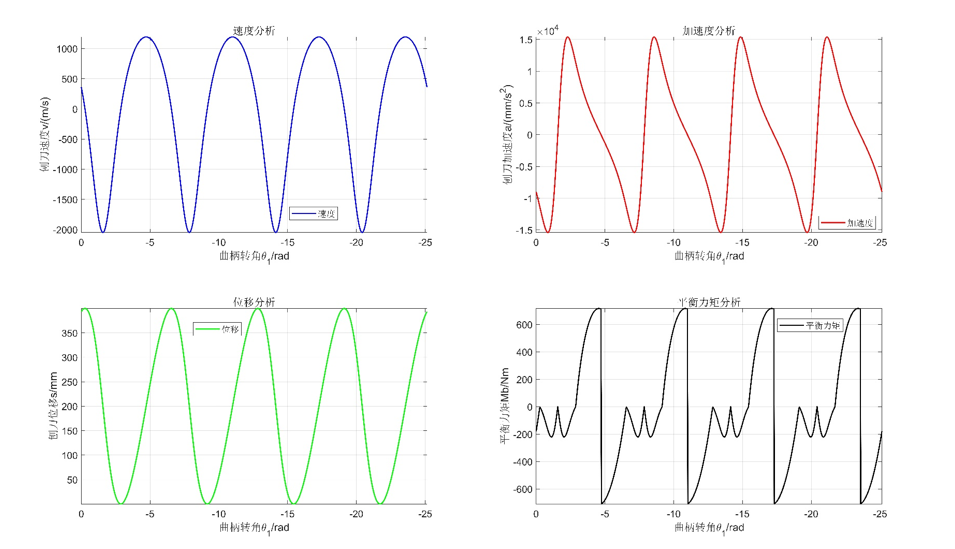
    subplot(2,2,1)
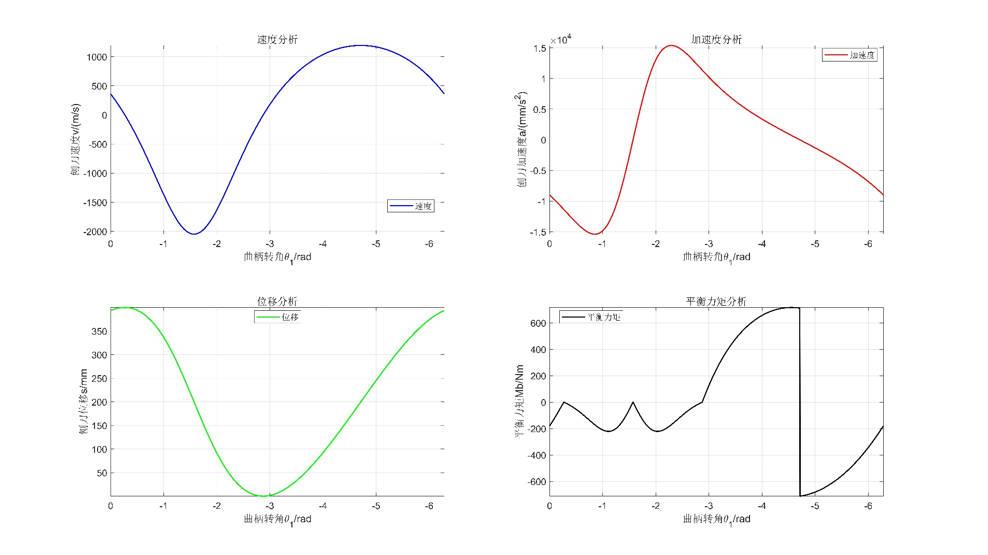
    plot(phy1_n,v,'LineWidth',1.5,'Color','b')
    title("速度分析",'FontSize',14)
    xlabel('曲柄转角\theta_1/rad','FontSize',12)
    ylabel('刨刀速度v/(m/s)','FontSize',12)
    hold on;
    grid on;
    axis tight;
    set(gca, 'XDir', 'reverse');
    set(gca, 'FontSize', 12)
    legend('速度','Location','best')
    
    subplot(2,2,2)
    plot(phy1_n,a,'LineWidth',1.5,'Color','r')
    title("加速度分析",'FontSize',14)
    xlabel('曲柄转角\theta_1/rad','FontSize',12)
    ylabel('刨刀加速度a/(mm/s^2)','FontSize',12)
    hold on;
    grid on;
    axis tight;
    set(gca, 'XDir', 'reverse');
    set(gca,'FontSize',12)
    legend('加速度','Location','best')
    
    subplot(2,2,3)
    plot(phy1_n,s,'LineWidth',1.5,'Color','g')
    title("位移分析",'FontSize',14)
    xlabel('曲柄转角\theta_1/rad','FontSize',12)
    ylabel('刨刀位移s/mm','FontSize',12)
    hold on;
    grid on;
    axis tight;
    set(gca, 'XDir', 'reverse');
    set(gca,'FontSize',12)
    legend('位移','Location','best')
    
    subplot(2,2,4)
    plot(phy1_n,Mb,'LineWidth',1.5,'Color','k')
    title("平衡力矩分析",'FontSize',14)
    xlabel('曲柄转角\theta_1/rad','FontSize',12)
    ylabel('平衡力矩Mb/Nm','FontSize',12)
    hold on;
    grid on;
    axis tight;
    set(gca, 'XDir', 'reverse');
    set(gca,'FontSize',12)
    legend('平衡力矩','Location','best')
    delete(gcp('nocreate'));
    pause;
end
if ifzu == 0
    % 独属于你的phy
    phy_for_you = input('输入你的角度(角度制),逆时针为正\n');
    phy1_wzr = phy_for_you*pi/180;
    [v_my,a_my,s_my,Mb_my,omegal3_my,alpha3_my,R_34_my,P_I3_my,M_I3_my,R_21_my] = sol_wzr(l1,l6,l3,omegal1,phy1_wzr,G5,G3,g,l_s3,J_s3)
    pause;
end

function [v,a,s,Mb,omegal3,alpha3,R_34,P_I3,M_I3,R_21] = sol_wzr(l1,l6,l3,omegal1,phy1,G5,G3,g,l_s3,J_s3)
 %% 运动求解
    % b3移动量求解
    sb = sqrt((l1*cos(phy1))^2 + (l6+l1*sin(phy1))^2);
    % phy3转角求解
    phy3 = acos(l1*cos(phy1)/sb);
    % v23、omegal3求解
    sol1 = [cos(phy3) -sb*sin(phy3);...
            sin(phy3) sb*cos(phy3)]\(omegal1 * l1*[-sin(phy1);cos(phy1)]);
    omegal3 = sol1(2);
    v23 = sol1(1);
    % a23、alpha3求解
    sol2 = [cos(phy3) -sb*sin(phy3);...
            sin(phy3)  sb*cos(phy3)]\...
        (-[-omegal3*sin(phy3) -v23*sin(phy3)-sb*omegal3*cos(phy3);...
          omegal3*cos(phy3) v23*cos(phy3)-sb*omegal3*sin(phy3)]*sol1 ...
        - omegal1^2*l1*[cos(phy1);sin(phy1)]);
    alpha3 = sol2(2);
    % 刨刀 v a s求解
    vd = -omegal3*l3;
    v = vd*sin(phy3);
    a = -omegal3^2*l3*cos(phy3) - alpha3*l3*sin(phy3);
    s = l3*cos(phy3)+200;

%% 力分析
    % 刨刀架分析
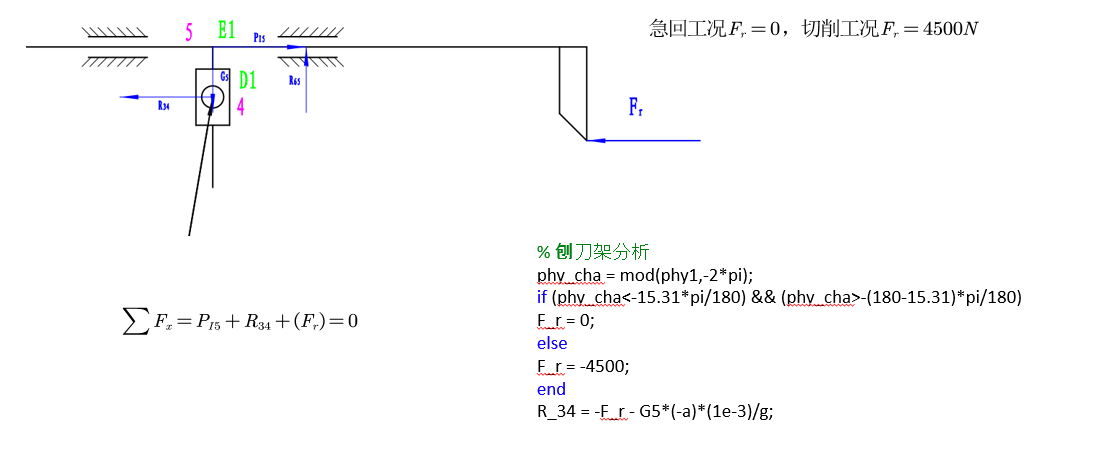
    phy_cha = mod(phy1,-2*pi);
    if (phy_cha<-15.31*pi/180) && (phy_cha>-(180-15.31)*pi/180)
        F_r = 0;
    else 
        F_r = -4500;
    end
    R_34 = -F_r - G5*(-a)*(1e-3)/g;
    % 导杆机构力分析
    R_43 = - R_34;
    % 构件3基本参数
    a_s3x = -l_s3*(1e-3)*(omegal3^2*cos(phy3)+alpha3*sin(phy3));
    a_s3y = -l_s3*(1e-3)*(omegal3^2*sin(phy3)-alpha3*cos(phy3));
    P_I3x = -G3*a_s3x/g;
    P_I3y = -G3*a_s3y/g;
    P_I3 = sqrt(P_I3x^2+P_I3y^2);
    M_I3 = -J_s3*alpha3;
%     %构件3待求变量
%     syms R_23x R_23y R_63x R_63y 
%     %4个未知量，自然就是4个方程了啊
%     eq1 = P_I3x+R_23x+R_63x+R_43 == 0;
%     eq2 = P_I3y+R_23y+R_63y-G3 == 0;
%     eq3 = - R_43*l_s3*(1e-3)*sin(phy3) - R_23x*(sb-l_s3)*(1e-3)*sin(phy3) + R_63x*l_s3*(1e-3)*sin(phy3)...
%           + R_23y*(sb-l_s3)*(1e-3)*cos(phy3) - R_63y*l_s3*(1e-3)*cos(phy3) + M_I3== 0;% 对s3取矩,def逆时针+
%     eq4 = R_23x*cos(phy3)+R_23y*sin(phy3) == 0;
%     sol3 = solve(eq1,eq2,eq3,eq4);
%     R_23x = double(sol3.R_23x);
%     R_23y = double(sol3.R_23y);

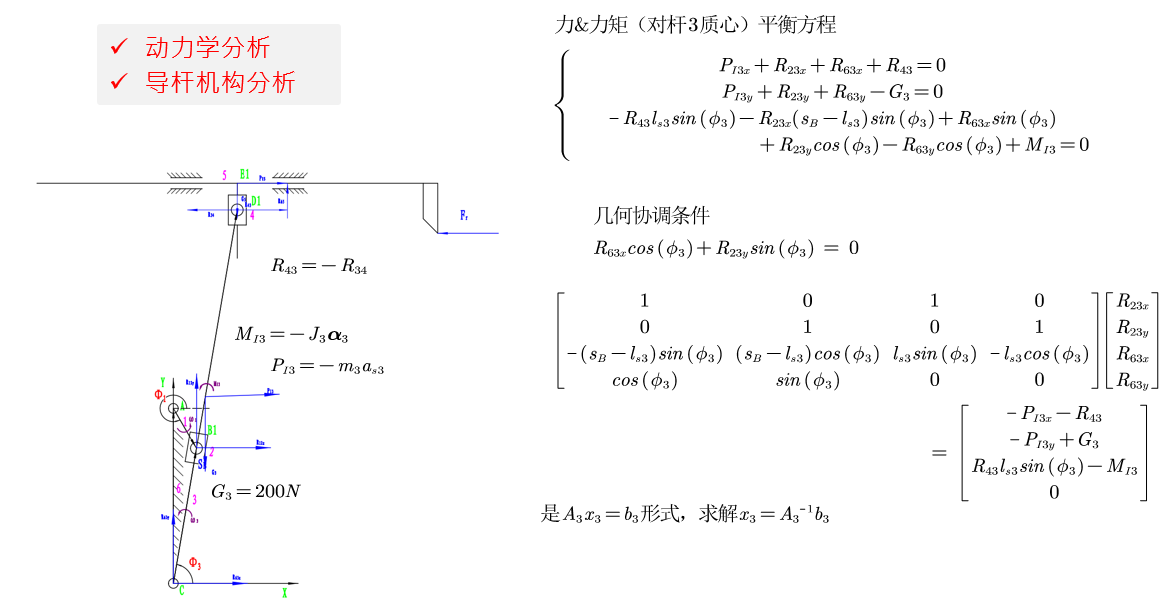
    sol3 = [1 0 1 0;
            0 1 0 1;
            -(sb-l_s3)*(1e-3)*sin(phy3) (sb-l_s3)*(1e-3)*cos(phy3) l_s3*(1e-3)*sin(phy3) -l_s3*(1e-3)*cos(phy3);...
            cos(phy3) sin(phy3) 0 0]\[-P_I3x-R_43;
                                      -P_I3y+G3;
                                      R_43*l_s3*(1e-3)*sin(phy3)-M_I3;
                                      0];
    R_23x = sol3(1);
    R_23y = sol3(2);
    %构件1、2
    R_21x = -R_23x;
    R_21y = -R_23y;
    R_21 = sqrt(R_21x^2+R_21y^2);
    %对支架取矩,def逆时针+
    if phy_cha <=0 && phy_cha >=-pi/2
        Mb = -R_21x*l1*(1e-3)*abs(sin(phy1))-R_21y*l1*(1e-3)*abs(cos(phy1));
    end
    if phy_cha <-pi/2 && phy_cha >=-pi
        Mb = R_21x*l1*(1e-3)*abs(sin(phy1))-R_21y*l1*(1e-3)*abs(cos(phy1));
    end
    if phy_cha <-pi && phy_cha >=-3*pi/2
        Mb = -R_21x*l1*(1e-3)*abs(sin(phy1))-R_21y*l1*(1e-3)*abs(cos(phy1));
    end
    if phy_cha <-3*pi/2 && phy_cha >=-2*pi
        Mb = R_21x*l1*(1e-3)*abs(sin(phy1))-R_21y*l1*(1e-3)*abs(cos(phy1));
    end
end
项目 > 压床设计
#原创
小型精刨机主切削运动机构
https://ysc2.github.io/ysc2.github.io/2024/04/13/小型精刨机主切削运动机构/
作者
Ysc
发布于
2024年4月13日
许可协议